Skip to main content

Get Support
Have a question? Let's get you an answer!

How Do I...? Troubleshooting Code & Webhooks Developer Zone

Other Help Resources
Wait, there's more! Check out these Community sourced spaces for additional resources.

Zapier Help Center Hire an Expert

Learning Resources
All of our best learning resources can be found here.

Featured Articles Show & Tell Zapier's products AI Hub Zapier Tools Hub

Share your knowledge
Give back to the Community by sharing your automation wins and helping to answer questions.

Share your success See unanswered questions User Groups

Other Learning Resources
Some of our favorite additional ways to upskill your Zapier knowledge.

Zapier Learn Zapier Blog Zapier Webinars

Product Updates
Check out what is new and upcoming with Zapier with our regular product updates.

Product Updates

Early Access Program
Want to join Early Access? Learn more here.

  • Home
  • Get Help
  • How Do I
  • 'Status Code 403 Forbidden' when trying to trying to email PDF reports from iAuditor

I’ve created many iAuditor zaps previously that generate a PDF report and email a copy (either on completion of an audit or when triggered by a failed response). Today I’ve been building a new conditional zap (using Paths) to email PDFs to different addresses based on filters within the audit(s). All tests are passed but when it comes to sending the emails it keeps failing. Initially I thought it may have been the 10 emails per hour limitation on the Email by Zapier task, but I just tried using Gmail instead but got the same error:

 

Clicking on ‘Troubleshoot error’ gives the following info:

 

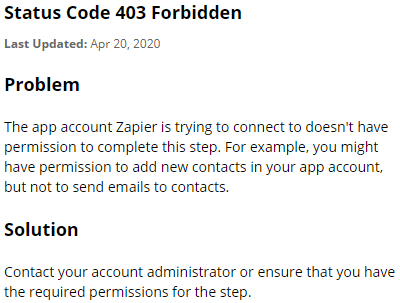
Any assistance would be appreciated!

Troubleshooting Tips

  1. Try deleting the entire step and adding it back
  2. Check your app authentications here: https://zapier.com/app/connections
  3. If you’re trying to use a Gmail account with @gmail.com there are limitations of approved apps: https://zapier.com/help/doc/common-problems-gmail#my-gmail-zap-has-an-error-about-connecting-to-google-approved-or-not-approved-apps

Troubleshooting Tips

  1. Try deleting the entire step and adding it back
  2. Check your app authentications here: https://zapier.com/app/connections
  3. If you’re trying to use a Gmail account with @gmail.com there are limitations of approved apps: https://zapier.com/help/doc/common-problems-gmail#my-gmail-zap-has-an-error-about-connecting-to-google-approved-or-not-approved-apps

Thanks for the tips @Troy Tessalone . I’ve just spent some considerable time with iAuditor support looking at this issue and have discovered that, despite the errors in testing, the Zap actually works just fine. Their advice follows:

I have confirmed with our senior support that the error in the steps when editing does not accurately reflect how the Zap will run when it comes to connecting with Gmail.

This is more to do with the Zapier connection than with iAuditor from what we've found out. 

I wouldn’t call this issue resolved as the testing error is still present, but at least I can now progress my work knowing that it will still function as expected.

Terms & Conditions